Unlocking the power of optimization is now easier than ever with the Solver Add-in. This guide provides a comprehensive walkthrough, from fundamental concepts to advanced techniques. Learn how to effectively leverage the Solver Add-in to tackle complex problems and discover optimal solutions within spreadsheets. Whether you’re a seasoned analyst or a beginner, this guide empowers you to harness the Solver Add-in’s potential for practical application.
This in-depth exploration covers everything from the basic setup and configuration of Solver problems to interpreting results and troubleshooting common issues. We’ll examine the different types of optimization problems solvable by the Solver Add-in, explore various algorithms, and illustrate the significance of appropriate settings. Real-world applications across diverse industries, including finance, engineering, and supply chain management, are highlighted to demonstrate the Solver Add-in’s wide-ranging utility.
Introduction to Solver Add-in
The Solver Add-in is a powerful tool within spreadsheet applications, primarily used for finding optimal solutions to complex problems. It automates the process of exploring various possibilities and identifying the best course of action based on specified constraints and objectives. This capability is particularly valuable in scenarios requiring mathematical optimization, allowing users to quickly explore different variables and arrive at the most efficient outcome.The Solver Add-in excels in situations where multiple factors interact to influence a desired outcome.
It’s particularly useful for decision-making in finance, operations research, engineering, and other fields where finding the best combination of resources or parameters is crucial. By systematically testing various possibilities, the Solver Add-in can reveal hidden relationships and trade-offs, ultimately leading to more informed and strategic decisions.
Purpose and Functionality
The Solver Add-in is a spreadsheet add-in that provides a user-friendly interface for solving optimization problems. It allows users to define an objective function, subject to various constraints, and then iteratively explores different solutions to find the optimal value. This functionality is embedded within the spreadsheet environment, allowing seamless integration with existing data and calculations. The Solver Add-in simplifies the process of finding optimal solutions by handling the complex calculations and iterations behind the scenes.
Typical Scenarios for Use
The Solver Add-in is beneficial in a wide array of scenarios, including:
- Resource Allocation: Determining the most efficient way to allocate limited resources (e.g., manpower, materials, budget) to achieve maximum output or minimum cost. For example, a manufacturing company might use Solver to determine the optimal production schedule that minimizes costs while meeting demand.
- Portfolio Optimization: Finding the optimal mix of investments to maximize returns while adhering to risk tolerance constraints. A financial advisor could use Solver to create a diversified investment portfolio that balances potential gains with the level of risk.
- Supply Chain Management: Optimizing the flow of goods and services through the supply chain to minimize costs and improve delivery times. A logistics company might use Solver to determine the most efficient transportation routes and warehousing strategies.
- Engineering Design: Finding the optimal design parameters for a product or system to maximize performance or minimize costs. An engineer might use Solver to determine the dimensions of a structural component that maximize strength while minimizing material usage.
History and Evolution
The Solver Add-in has evolved alongside advancements in spreadsheet software. Initially introduced as a part of Microsoft Excel, it has undergone continuous refinement and improvements. The add-in has become a crucial tool for decision-making, addressing increasingly complex optimization problems as computing power has increased. The iterative approach used by Solver allows for a more precise determination of optimal solutions compared to simpler methods.
Key Concepts in Optimization Problems
The Solver Add-in addresses optimization problems by focusing on several key concepts. These include:
- Objective Function: This function defines the quantity to be optimized (maximized or minimized). It quantifies the desired outcome, such as profit, cost, or distance.
- Decision Variables: These are the controllable inputs or factors that influence the objective function. They represent choices that can be adjusted to achieve the optimal outcome.
- Constraints: These are limitations or restrictions on the decision variables. They represent real-world limitations, such as budget constraints, resource availability, or legal regulations. For example, a production schedule might be constrained by the number of available workers and the amount of raw materials.
Types of Optimization Problems
The Solver Add-in can handle various types of optimization problems. The table below Artikels the common categories.
| Problem Type | Description |
|---|---|
| Linear Programming | Optimization problems where the objective function and constraints are linear functions of the decision variables. |
| Nonlinear Programming | Optimization problems where the objective function or constraints are nonlinear functions of the decision variables. These problems are often more complex to solve. |
| Integer Programming | Optimization problems where some or all of the decision variables must take on integer values. This is relevant in scenarios involving discrete choices, like choosing a specific number of items or machines. |
| Mixed Integer Programming | A combination of linear or nonlinear programming where some variables are constrained to integer values, while others are continuous. |
Setting up a Solver Problem
The Solver Add-in in spreadsheet applications provides a powerful tool for finding optimal solutions to complex problems. Setting up a Solver problem involves meticulously defining the objective, variables, and constraints. This section details the process, enabling users to effectively leverage Solver for various optimization tasks.Defining the objective, variables, and constraints is crucial for a successful Solver optimization. Understanding these components allows users to tailor the Solver to their specific needs, resulting in accurate and relevant optimal solutions.
Accessing the Solver Add-in
Different spreadsheet applications have slightly varied methods for accessing the Solver Add-in. Typically, users navigate to the “Add-ins” or “Tools” menu and select the Solver option. This often requires enabling the Solver Add-in if it isn’t already active within the application. Specific instructions are readily available within the application’s help documentation.
Defining the Objective Cell
The objective cell represents the cell containing the value that Solver aims to maximize or minimize. Carefully select the appropriate cell reflecting the target outcome. For instance, if optimizing profit, the objective cell would likely contain the calculated profit value.
Specifying Changing Cells
Changing cells, also known as decision variables, are the cells Solver will adjust to achieve the optimal objective value. These cells represent the unknowns in the problem. For instance, if determining the optimal production levels of different products, the changing cells would contain the quantities of each product to be manufactured.
Defining Constraints
Constraints are limitations imposed on the changing cells. These can take various forms, ensuring the solution remains within realistic bounds.
- Non-negativity Constraints: These ensure that the changing cells do not take on negative values, a common requirement in many optimization problems. For example, production quantities cannot be negative.
- Integer Constraints: These specify that the changing cells must take on integer values, crucial in situations where quantities are discrete (e.g., the number of units to be produced).
- Binary Constraints: These constraints force the changing cells to be either 0 or 1, commonly used for yes/no decisions (e.g., whether to build a new factory).
- Other Constraints: Other constraints may involve specific relationships between changing cells, like resource limitations (e.g., a maximum amount of raw materials available), or upper and lower bounds (e.g., a minimum and maximum production target). These constraints are tailored to the specific problem being solved.
Specifying the Optimization Goal
The optimization goal dictates whether Solver should maximize or minimize the objective cell. This decision depends on the nature of the problem. For example, maximizing profit or minimizing costs.
Realistic Optimization Scenarios
The following table illustrates diverse scenarios where Solver can be applied:
| Scenario | Objective | Changing Cells | Constraints |
|---|---|---|---|
| Production Planning | Maximize Profit | Production quantities of different products | Raw material availability, labor hours, production capacity |
| Portfolio Optimization | Maximize Return | Investment allocations across different assets | Budget constraints, risk tolerance |
| Supply Chain Management | Minimize Transportation Costs | Shipment routes and quantities | Delivery deadlines, capacity of vehicles |
| Resource Allocation | Minimize Project Completion Time | Task assignments and scheduling | Task dependencies, resource availability |
Solver Parameters and Options

The Solver add-in provides a flexible platform for optimization, but effective use hinges on understanding and adjusting its parameters and options. Proper selection significantly impacts the accuracy and efficiency of the solution process. Careful consideration of these settings is crucial to achieving optimal results within a reasonable timeframe.The Solver add-in offers a range of algorithms to tackle diverse optimization problems.
Choosing the right algorithm, along with adjusting tolerances and iterations, can drastically affect the Solver’s performance and the quality of the obtained solution. Different algorithms excel in different scenarios, and understanding their strengths and weaknesses allows users to select the most appropriate method for their specific needs.
Available Algorithms
Various algorithms are available within the Solver add-in, each with its own strengths and weaknesses. These algorithms employ different approaches to find optimal solutions, impacting the speed and accuracy of the process.
- GRG Nonlinear: This algorithm is a popular choice for nonlinear optimization problems. It uses a gradient-based method to iteratively approach the optimal solution. Its strength lies in its ability to handle complex, nonlinear relationships. However, it might not be suitable for problems with multiple local optima, where it could converge to a suboptimal solution instead of the global optimum.
- LP Simplex: This algorithm is tailored for linear programming problems. It is generally very efficient and reliable for this type of optimization. Its simplicity and direct approach often lead to rapid convergence for linear models.
- Evolutionary: This algorithm is a robust method for both linear and nonlinear problems. It employs a heuristic approach, simulating natural selection to explore the solution space. Its strength lies in its ability to potentially find global optima, even in complex, multimodal landscapes. However, it typically requires more computational resources and time than other algorithms, particularly for larger problems.
Tolerance and Iteration Settings
The Solver add-in allows users to set tolerances and maximum iterations. These parameters directly influence the optimization process and the accuracy of the results.
- Tolerance: The tolerance setting defines the acceptable degree of error in the solution. A lower tolerance value generally leads to a more precise solution but may increase the computational time. A higher tolerance may result in a less precise solution but might finish faster.
- Iterations: The maximum number of iterations specifies the upper limit for the optimization process. Exceeding this limit can cause the Solver to stop prematurely, potentially resulting in an incomplete or inaccurate solution. Choosing an appropriate number of iterations requires balancing accuracy and computational time.
Impact of Solution Methods
Different solution methods can significantly influence the outcome of the optimization process. The choice of algorithm, tolerance, and iterations profoundly affects the quality and time taken to obtain a solution.
- Comparison: For instance, when dealing with a linear programming problem, the LP Simplex algorithm is often preferred due to its efficiency and proven track record in this type of problem. However, for a nonlinear optimization problem with multiple local optima, the GRG Nonlinear algorithm, despite its potential for faster convergence to a local optimum, might require additional analysis to ensure the global optimum is achieved.
Solver Options and their Effect
The Solver add-in offers various options that can further customize the optimization process. Selecting the right options ensures the algorithm efficiently finds the optimal solution while also considering the user’s specific needs and constraints.
- Assumptions: Correctly setting the assumptions for the problem ensures the solver operates on the intended parameters and constraints. Incorrect assumptions can lead to unexpected or inaccurate results. Consider the variables and relationships between them when defining assumptions for the solver.
- Constraints: Correctly setting constraints is crucial to ensure the optimization process remains within the acceptable boundaries of the problem. Inappropriate constraints can restrict the Solver’s ability to find a suitable solution. Reviewing the defined constraints to ensure they are valid and align with the problem’s requirements is essential.
Interpreting Solver Results
After successfully running the Solver add-in, interpreting the results is crucial for understanding the optimal solution’s implications. This involves not only identifying the optimal values but also assessing the robustness and feasibility of the solution within the defined constraints. A thorough analysis of the Solver output allows for informed decision-making based on the results.
Optimal Solution Values
The Solver output provides the optimal values for the changing cells, representing the best possible outcome within the specified constraints. These values are crucial for implementing the solution in a real-world context. Understanding how the changing cells are affected by the constraints is key to understanding the sensitivity of the solution.
Sensitivity Analysis
Analyzing the sensitivity of the optimal solution involves assessing how changes in the constraints impact the optimal values. This analysis helps determine the robustness of the solution. For instance, if a small change in a constraint significantly alters the optimal values, the solution might be less reliable. A thorough sensitivity analysis helps evaluate the stability of the optimal solution.
Feasibility of the Optimal Solution
Evaluating the feasibility of the optimal solution requires confirming that the solution adheres to all the defined constraints. The Solver output should clearly indicate whether the solution satisfies all the limitations. If the solution violates any constraints, it is not feasible and needs to be revisited. By verifying the solution’s feasibility, we can ensure the practical application of the results.
Example Table of Solver Results Interpretation
| Scenario | Changing Cells | Optimal Values | Constraints | Feasibility | Sensitivity Analysis |
|---|---|---|---|---|---|
| Production Planning | Units of Product A, Units of Product B | Product A: 1000 units, Product B: 1500 units | Labor hours: 1000 hours, Raw material: 2000 units | Feasible – all constraints met | Slight increase in labor hours (1050 hours) results in a minimal change in optimal production. Significant increase in raw materials would affect optimal solution. |
| Portfolio Optimization | Investment in Stock X, Investment in Stock Y | Stock X: $50,000, Stock Y: $75,000 | Total Investment: $125,000, Minimum Return: 8% | Feasible – all constraints met | Decreasing the total investment limit to $100,000 leads to a re-allocation of investment across stocks. |
| Budget Allocation | Marketing Spend, Research & Development Spend | Marketing: $20,000, R&D: $15,000 | Total Budget: $35,000, Minimum Marketing Spend: $10,000 | Feasible – all constraints met | Reducing the total budget to $30,000 necessitates a proportional reduction in both marketing and R&D spend. |
Advanced Solver Techniques

The Solver add-in, while powerful for basic optimization problems, becomes even more valuable when tackling complex scenarios. This section explores advanced techniques to leverage Solver’s capabilities for intricate models, including handling multiple constraints, non-linear relationships, integer/binary constraints, and multiple decision variables. These techniques allow for a deeper understanding and application of optimization in a wider range of problem domains.
Handling Multiple Constraints and Objectives
Multiple constraints and objectives are frequently encountered in real-world optimization problems. Solver can effectively manage these by incorporating multiple conditions and goals into the model. Understanding how to combine and prioritize these elements is crucial for achieving the desired outcome. For example, a manufacturing company might want to minimize production costs while simultaneously meeting specific quality standards and delivery deadlines.
Each of these factors represents a constraint or an objective within the model.
Handling Non-Linear Relationships
Many real-world relationships are not linear. Solver can accommodate non-linear functions, allowing for greater model accuracy and flexibility. Recognizing these non-linear relationships is crucial for developing an appropriate model. For instance, the relationship between production output and resource consumption might be non-linear, with diminishing returns as production scales. Solver can handle these scenarios by incorporating non-linear functions into the objective function or constraints.
For example, consider the quadratic function: f(x) = ax 2 + bx + c.
Managing Integer or Binary Constraints
Integer or binary constraints are essential for scenarios where decision variables must take on whole number values (e.g., the number of machines to purchase) or binary values (e.g., whether a particular product line should be included). Solver’s integer optimization capabilities address these needs. The addition of integer or binary constraints significantly alters the solution space and necessitates specialized techniques to find the optimal solution within these restrictions.
For instance, a company deciding whether to open a new store in a given location would have a binary variable that could take on the values of 1 (open) or 0 (not open).
Utilizing Solver with Multiple Decision Variables
Complex problems often involve numerous decision variables. Solver can handle these situations effectively, allowing for a comprehensive analysis of various choices. A typical example is resource allocation. For instance, a portfolio manager might need to allocate funds to various investment options with different expected returns and risk levels. This involves numerous decision variables (amount invested in each option) and requires an understanding of how to formulate the problem for Solver.
Troubleshooting Common Issues

The Solver Add-in, while powerful, can sometimes encounter difficulties. Understanding common errors and their solutions is crucial for effective problem-solving. This section provides strategies for identifying and resolving these issues, allowing you to maximize the utility of the Solver Add-in.Troubleshooting Solver issues involves a systematic approach. Reviewing constraints, settings, and the input data can often pinpoint the source of the problem.
Accurate interpretation of error messages is key to efficient resolution.
Common Solver Errors and Their Solutions
Troubleshooting Solver issues often begins with understanding the error messages. These messages, while sometimes cryptic, provide valuable clues to the underlying problem.
- Solver Cannot Find a Feasible Solution: This error indicates that no solution exists within the defined constraints. Possible causes include overly restrictive constraints or inconsistent data. To troubleshoot, review each constraint carefully. Ensure that the constraints are realistic and not mutually exclusive. Verify the data input for accuracy and completeness.
If possible, relax some constraints temporarily to see if a solution becomes available. This process helps in isolating the problematic constraint(s). For instance, if a constraint on the production of two products simultaneously is unrealistic, relax the constraint to observe if the solver finds a solution with only one product.
- Solver Could Not Find a Solution: This is a general error indicating a failure to find a solution within the time limit or using the specified algorithm. Potential reasons include excessively complex problems, unsuitable algorithms, or issues with the data or model structure. Review the problem setup for complexity. Ensure the model structure is well-defined and avoids unnecessary complexity. Consider changing the algorithm or increasing the maximum iterations allowed.
Also, ensure data accuracy and check for circular references or redundant constraints.
- Solver Error: Numerical Problem: This error typically arises from numerical instability in the solution process. This is often caused by extremely large or small numbers, or by very sensitive or ill-conditioned problems. Strategies include scaling the variables or constraints to a more manageable range. Check for extremely large or small values in the input data. Use appropriate scaling factors to bring values into a more normalized range.
If the problem involves multiple products, examine the ratio of their prices and demands, as these can cause numerical instability.
Interpreting Solver Error Messages
Error messages from the Solver Add-in can be quite specific. A methodical approach to interpreting these messages is crucial for efficient troubleshooting. The message often contains hints about the source of the problem, such as referencing a specific constraint or a range of values. Carefully read the entire error message and note any specific references to cells or formulas.
Troubleshooting Table
| Error | Possible Causes | Troubleshooting Steps |
|---|---|---|
| Solver Cannot Find a Feasible Solution | Overly restrictive constraints, inconsistent data | Review constraints, verify data accuracy, relax constraints temporarily |
| Solver Could Not Find a Solution | Complex problem, unsuitable algorithm, data/model issues | Simplify model, change algorithm, increase iterations, verify data |
| Solver Error: Numerical Problem | Large/small numbers, sensitive/ill-conditioned problem | Scale variables/constraints, check for extreme values, review model |
Real-World Applications
The Solver Add-in transcends theoretical exercises, proving invaluable in a multitude of real-world scenarios. Its ability to find optimal solutions across various industries makes it a powerful tool for informed decision-making. This section explores practical applications, illustrating how businesses leverage Solver to optimize their operations and achieve significant gains.
Optimization of Product Mix
Determining the optimal product mix is a critical challenge for manufacturers and businesses. Solver helps determine the most profitable combination of products given constraints on resources like raw materials, labor, and production capacity. For instance, a furniture manufacturer might use Solver to identify the optimal quantities of chairs, tables, and sofas to produce, maximizing profits while adhering to material availability and production time limits.
Solver can evaluate different production scenarios and pinpoint the most profitable mix.
Resource Allocation
Effective resource allocation is essential for efficient operations. Solver can be employed to optimize the allocation of resources like personnel, equipment, and time to meet project goals. Consider a construction company needing to schedule workers for different tasks. Solver can analyze worker skills, project deadlines, and equipment availability to create the most efficient schedule. By evaluating various scenarios, Solver can help allocate resources optimally, minimizing delays and maximizing productivity.
Investment Portfolio Optimization
In finance, Solver plays a crucial role in optimizing investment portfolios. Investors can use Solver to determine the optimal mix of stocks, bonds, and other assets that balances risk and return. By considering factors like historical performance, correlation, and market volatility, Solver can identify the most suitable portfolio strategy for an investor’s specific goals. This ensures the portfolio aligns with risk tolerance and maximizes potential returns.
Translation of Business Problems into Optimization Models
A critical step in utilizing Solver is translating a business problem into an optimization model. This involves defining decision variables, objective functions, and constraints. For instance, a retailer might want to optimize their inventory levels. The decision variables would be the quantity of each product to stock. The objective function could be to minimize inventory costs while ensuring sufficient stock to meet demand.
Constraints would include storage space limitations, order quantities, and predicted demand.
Solver’s Role in Decision-Making Processes
Solver empowers decision-makers with data-driven insights by providing optimal solutions to complex problems. It allows for systematic analysis of various scenarios, leading to well-informed choices. The output from Solver can guide strategic planning, resource allocation, and operational efficiency. By quantifying the impact of different decisions, Solver facilitates more informed and effective business strategies.
Real-World Applications Table
| Real-World Application | Problem | Solver Solution | Benefits Achieved |
|---|---|---|---|
| Product Mix Optimization (Furniture Manufacturer) | Maximize profits while respecting material and production capacity constraints. | Solver identifies optimal production quantities of chairs, tables, and sofas. | Increased profitability, efficient resource utilization, reduced waste. |
| Resource Allocation (Construction Company) | Efficiently schedule workers and equipment for various tasks while meeting project deadlines. | Solver creates an optimized schedule considering worker skills, project timelines, and equipment availability. | Reduced project delays, improved productivity, and enhanced project management. |
| Investment Portfolio Optimization (Investor) | Balance risk and return by selecting the optimal mix of stocks, bonds, and other assets. | Solver identifies the optimal asset allocation strategy based on historical data, correlations, and market volatility. | Enhanced portfolio performance, reduced risk, and optimized returns. |
Summary
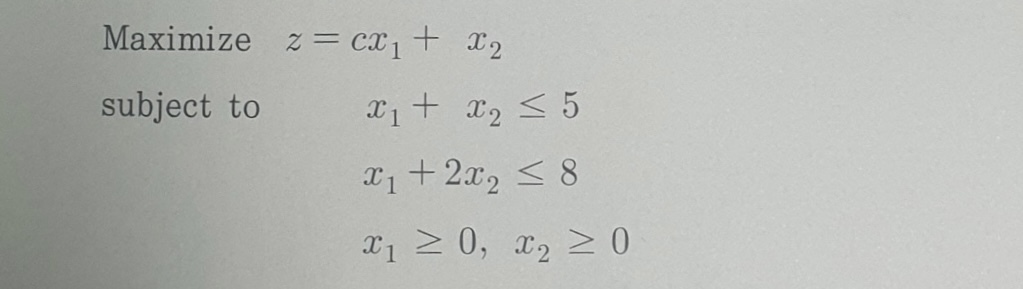
In conclusion, this guide has presented a comprehensive approach to leveraging the Solver Add-in for optimal solutions. By understanding the underlying concepts, mastering the setup process, interpreting results, and employing advanced techniques, you can effectively solve a wide range of optimization problems. The guide’s emphasis on real-world applications and troubleshooting ensures a practical understanding, equipping you to confidently use the Solver Add-in to drive informed decision-making in various fields.